

So, in your circuit, there is only one path. Thsi is different than an element on the main way and then a bifurcation, that's nothing. The bifurcation must be BEFORE the elements, so that each element is already in a branch.

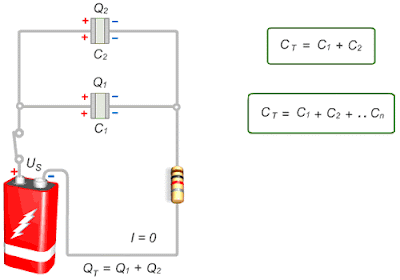
If there's one element and then the bifurcation, that's nothing. (This can be generalized to whatever number of branches). In the road analogy, you'd need to have one village on the left path and another on the right path. This implies that there must be a bifurcation. On the other hand, two elements are in parallel when each element is in a different branch of the circuit. If the road goes through two villages, and there is only one road, it is series. When capacitors are connected together in parallel the total or equivalent capacitance, CT in the circuit is equal to the sum of all the individual capacitors. No matter how far they are, if there is only one way, you cannot avoid any element, they are in series. When capacitors are connected in parallel, the potential difference V across each is the same and the charge on C1, C. There is only one path, so, if you follow the wire, you will find the first element and then the second element. For a charged capacitor, the general relationship between its charge Q, its capacitance C, and its potential difference V is: QCV.
#Capacitors in parallel series#
Two elements are in series if they are one after another. How can you tell? This is a rule of thumb: you have to check if there is more than one possible path. IT doesn't matter if they are upside or in the red boxes, it's series. In your case, both capacitos are in series. With capacitors, its the reverse: parallel connections result in additive values while series connections result in diminished values.There are no dumb questions, just bad teachers. With resistors, series connections result in additive values while parallel connections result in diminished values. The formula for calculating the parallel total capacitance is the same form as for calculating series resistances:Īs you will no doubt notice, this is exactly the opposite of the phenomenon exhibited by resistors. Thus, the total capacitance is more than any one of the individual capacitors’ capacitances. As we’ve just seen, an increase in plate area, with all other factors unchanged, results in increased capacitance. (The 10m (10 milliohm) resistor is there to get around a problem with the simulator.) Next: Thevenins Theorem. If two or more capacitors are connected in parallel, the overall effect is that of a single equivalent capacitor having the sum total of the plate areas of the individual capacitors. This demonstrates that the capacitance of two capacitors in parallel is equal to the sum of the two separate capacitances. When capacitors are connected in parallel, the total capacitance is the sum of the individual capacitors’ capacitances. If two or more capacitors are connected in parallel, the overall effect is that of a single equivalent capacitor having the sum total of the plate areas of the individual capacitors. The formula for calculating the series total capacitance is the same form as for calculating parallel resistances: When capacitors are connected in parallel, the total capacitance is the sum of the individual capacitors’ capacitances. As with resistors, two commonly encountered configurations for capacitors are the parallel and series.
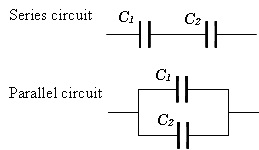
Thus, the total capacitance is less than any one of the individual capacitors’ capacitances. Many different types of connections are possible. As we’ve just seen, an increase in plate spacing, with all other factors unchanged, results in decreased capacitance. If two or more capacitors are connected in series, the overall effect is that of a single (equivalent) capacitor having the sum total of the plate spacings of the individual capacitors. When capacitors are connected in series, the total capacitance is less than any one of the series capacitors’ individual capacitances.


 0 kommentar(er)
0 kommentar(er)
